Let ![]() be a variable defined on a 3D hybride grid.
Consider a regular lon/lat grid cell with area
be a variable defined on a 3D hybride grid.
Consider a regular lon/lat grid cell with area
![]() between halflevels
between halflevels
![]() .
The field weighted with the mass is to be computed from:
.
The field weighted with the mass is to be computed from:
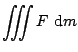 |
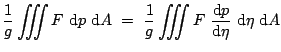 |
(3.37) | |
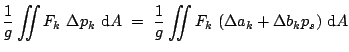 |
(3.38) | ||
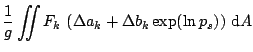 |
(3.39) | ||
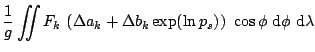 |
(3.40) |
| (3.41) |