Mathematics of Planet Earth

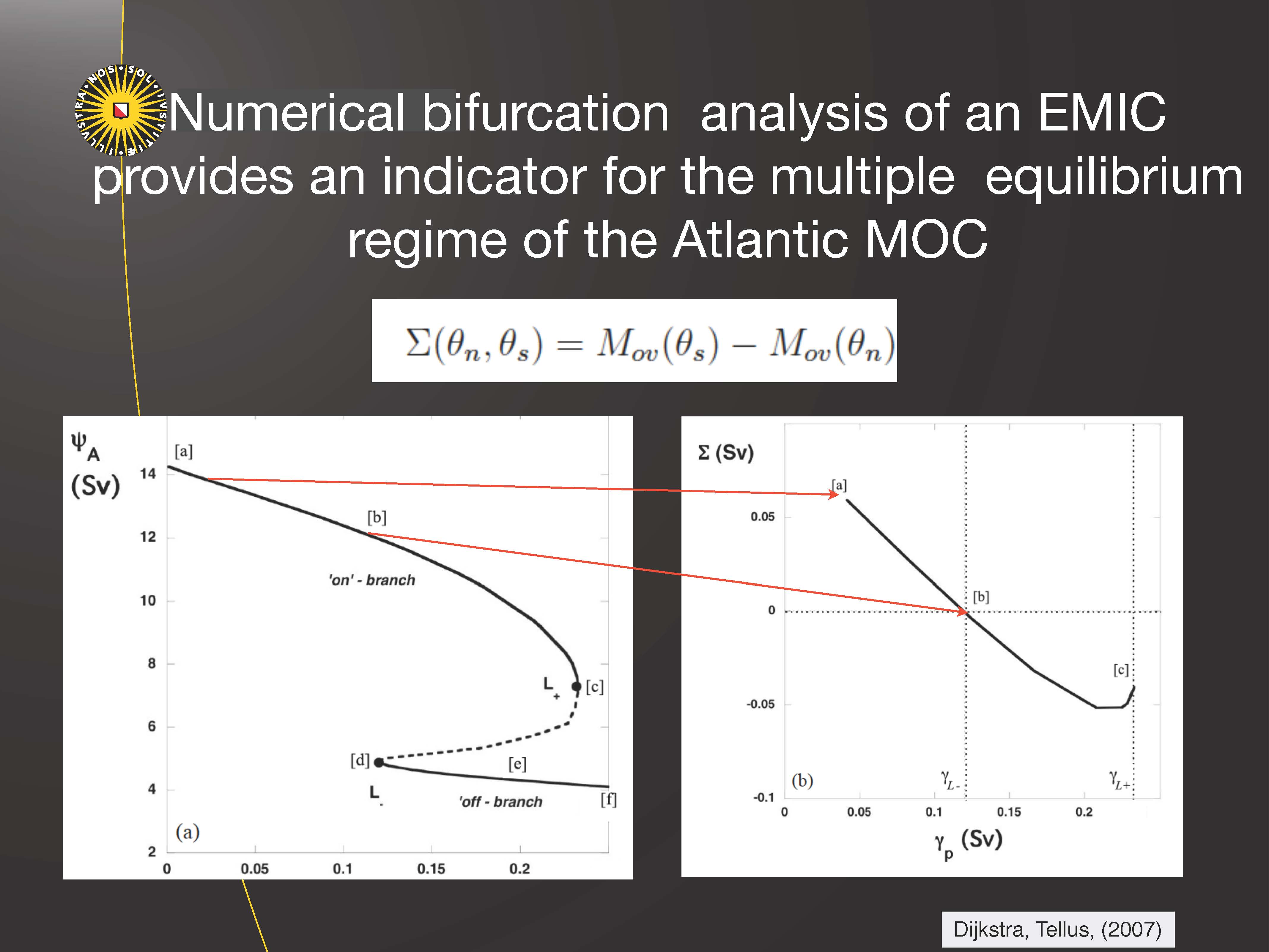
Much remains to be done to provide the proper mathematical theory of climate variability and change. We aim to contribute to this theory from a dynamical systems angle, focusing on bifurcation theory and ergodic theory of partial differential equation models of the climate system.

Intrinsic Variability in the Climate System

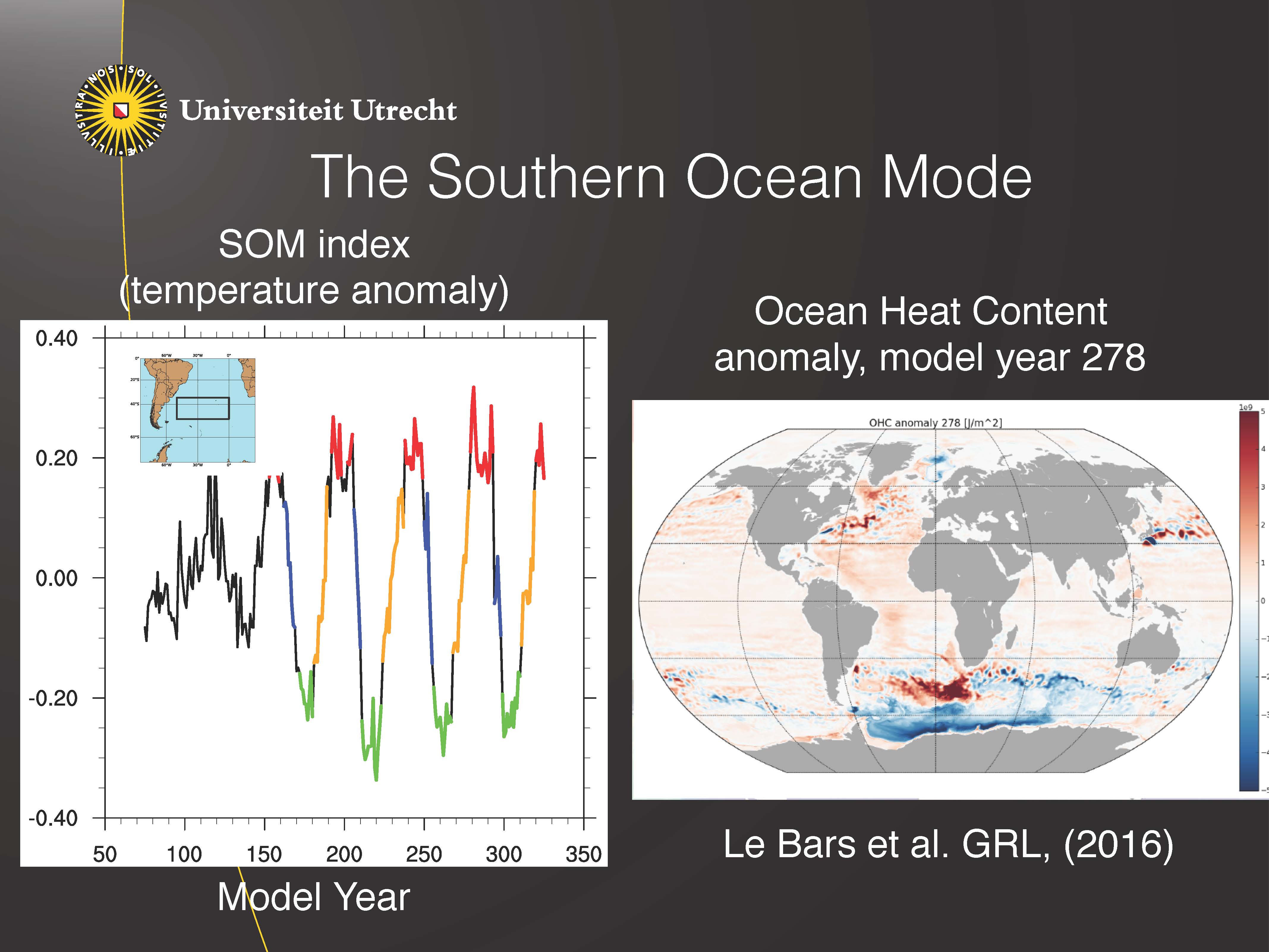
A diverse set of climate feedbacks leads to a wide spectrum of intrinsic variability in the climate system, with as prominent example the El Nino-Southern Oscillation. We aim to contribute to the understanding of the mechanisms of this variability, using a hierarchy of models, from conceptual climate models to high-resolution global climate models.

Turbulence and Mixing in Oceans and Lakes

The representation of subgrid-scale mixing processes in large-scale ocean and lake models is one of the barriers for progress in physical oceanography and limnology. We aim to contribute to this theme by studying specific cases (Eastern North Atlantic, Lake Garda) both observationally (using a microstructure profiler) and numerically.

Contact person

Contact person for this theme is prof Henk Dijkstra.

Group members

Current group members are listed here.

Current projects

Find ongoing projects here.