

Next: Spectral fields
Up: Grids and transformations
Previous: Grids and transformations
Longitude-latitude coordinates
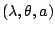 are defined
with
are defined
with
![$\lambda\in[-\pi,\pi]$](img10.gif) the longitude,
the longitude,
![$\theta\in[-\pi/2,\pi/2]$](img11.gif) the latitude, and
the latitude, and 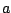 the radius of the earth.
A new latitude coordinate
the radius of the earth.
A new latitude coordinate 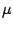 is introduced:
is introduced:
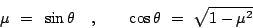 |
(3.1) |
Table 3.1 lists the coordinate transformations
from 2D carthesian to spherical.
Table 3.1:
Coordiante transformations from 2D carthesian to spherical.
| |
|
|
|
| |
carthesian |
spherical |
spherical,
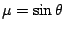 |
| |
|
|
|
| |
|
|
|
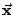 |
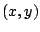 |
 |
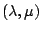 |
| |
|
|
|
| |
|
|
|
| |
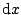 |
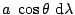 |
|
| |
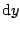 |
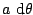 |
|
| |
|
|
|
| |
|
|
|
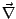 |
 |
 |
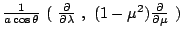 |
| |
|
|
|
| |
|
|
|
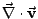 |
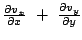 |
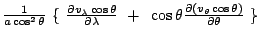 |
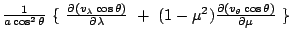 |
| |
|
|
|
|


Next: Spectral fields
Up: Grids and transformations
Previous: Grids and transformations
TM5
2009-03-03
![]() are defined
with
are defined
with
![]() the longitude,
the longitude,
![]() the latitude, and
the latitude, and ![]() the radius of the earth.
A new latitude coordinate
the radius of the earth.
A new latitude coordinate ![]() is introduced:
is introduced: