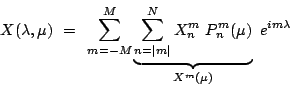 |
(3.2) |
References: [Davies, 1990]
The ECMWF definition of a spherical harmonic function is the following:
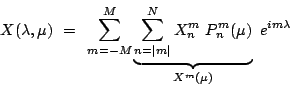 |
(3.2) |
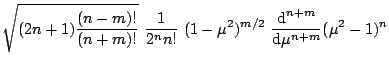 |
(3.3) | ||
| (3.4) |
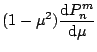 |
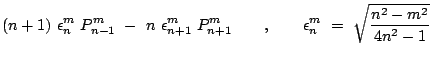 |
(3.5) |
| (3.6) |
The sperical harmonics are eigenfunction of the Laplacian operator on the
sphere:
The "Fourrier coefficients" ![]() are usefull for evaluation
of the spherical harmonics:
are usefull for evaluation
of the spherical harmonics:
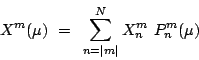 |
(3.8) |
| (3.9) |
Use Fast Fourrier Transform to evaluate at ![]() equiradial
spaced longitudes including zero:
equiradial
spaced longitudes including zero:
| (3.10) | |||
| (3.11) | |||
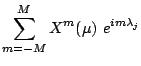 |
(3.12) | ||
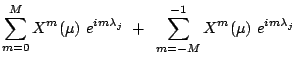 |
(3.13) | ||
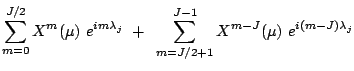 |
(3.14) | ||
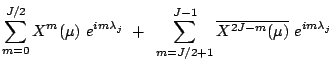 |
(3.15) | ||
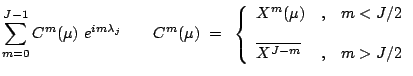 |
(3.16) | ||
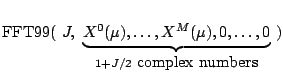 |
(3.17) |
The Fourrier coefficients ![]() are usefull for evaluation
of
are usefull for evaluation
of
![]() at oposite latitudes and multiple longitudes.
Split in even and odd summation:
at oposite latitudes and multiple longitudes.
Split in even and odd summation:
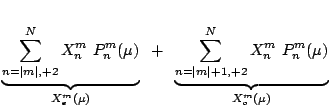 |
(3.18) | ||
| (3.19) |
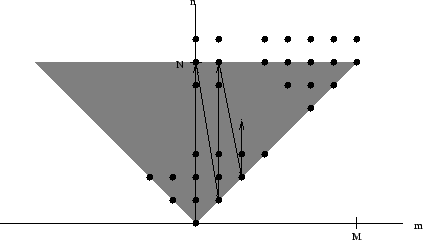
The ECMWF models uses a triangular truncation ![]() , see figure 3.1.
, see figure 3.1.
 |
Application of the nabla-operator to spherical harmonics
(3.1) requires partial derivatives
to ![]() and
and ![]() (table 3.1):
(table 3.1):
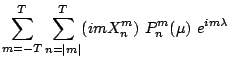 |
(3.21) |
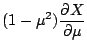 |
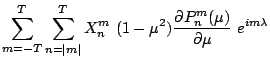 |
(3.22) | |
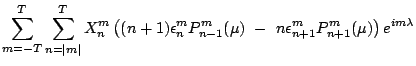 |
(3.23) | ||
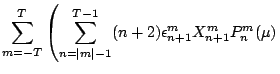 |
(3.24) | ||
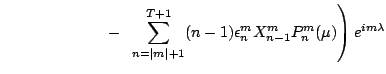 |
(3.25) | ||
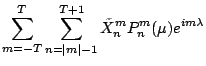 |
(3.26) | ||
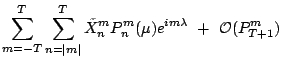 |
(3.27) |
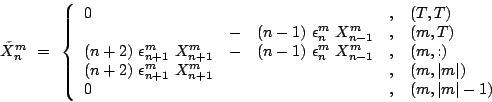 |
(3.28) |
Quote from [Riddaway and Hortal, 2001], section 6.2:
It can be shown that, starting from the set ofcomplex Fourrier coefficients
going to the set ofgrid points
and returning to, we recover exactly the original values (the transforms are exact) as long as
and the points are equally spaced in
. This distribution of points with
is known as the linear grid.
On the other hand it can be shown also that the product of two functions can be computed without aliassing by the transform method of transforming both functions to grid-point space, multiplying together the functions at each grid-point and transforming back the product to Fourier space, as long as. The distribution of points for which
is known as the quadratic grid.
Quote from [Riddaway and Hortal, 2001], section 6.6:
The integral with respect to the latitude can be performed from the Fourier coefficients by means of a Gaussian quadrature formula and it can be shown that this integral is exact if the latitudes at which the input data are given are taken at the points where
(these are called the Gaussian latitudes) with. Furthermore products of two functions can be computed alias-free if the number of Gaussian latitudes is
. The Gaussian latitudes are not equally spaced as the points to compute the discrete Fourier transforms but they are nearly so and therefore this spacing is approximately the same as the longitudinal spacing.
The distribution of points allowing exact transforms is called the linear Gaussian grid and it has at leastlongitude points equally spaced at each of at least
Gaussian latitude rows. Products of two functions can be computed alias-free if we use a quadratic Gaussian grid which is made of at least
equally spaced points in each of at least
Gaussian latitudes.
The same distribution of grid-points of a Gaussian grid can represent a linear or a quadratic Gaussian grid depend-ing on the spectral truncation used in conjunction with that grid. As an example, the quadratic grid corresponding to a spectral truncation of T213 coincides with the linear Gaussian grid corresponding to the spectral truncation T319.