| task | description |
|---|---|
| pv | potential vorticity |
| pvth | potential vorticity, potential temperature ('theta'), eqv. lat of pv on theta levels |
The content version is an attribute in hdf files.
| content version | description |
|---|---|
| 10 | initial number pv (march 2003) |
| 10 | initial number pvth (oct 2003) |
| file | param | description | unit | shape | time res. (hr) | grib code | hor. comb. | vert. comb | Comments |
|---|---|---|---|---|---|---|---|---|---|
| pv | pv | potential vorticity | K m2/kg/s | im x jm x lm | [21,03], .. | 060 | mass aver | mass aver | |
| pvth | pv | potential vorticity | K m2/kg/s | im x jm x lm | [21,03], .. | mass aver | mass aver | ||
| theta | potential temperature | K | im x jm x lm | [21,03], .. | mass aver | mass aver | |||
| eqvlatb | boundaries of eqv. lat. bins | deg | 0:jm x ntheta | [21,03], .. | |||||
| eqvinds | index of eqv. lat. bin | index | im x jm x ntheta | ||||||
Potential vorticity fields are valid for 6 hour intervals.
Computed from ECMWF fields valid for the mid of the interval. First computed on ECMWF's Gaussian Grid, then mass weighted average over cells and layers.

Definition according to [Holton, 1992, §4.3]:
| (4.1) |
| (4.2) |
| (4.3) |
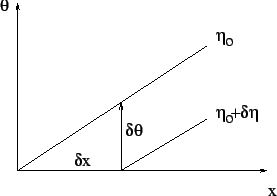
Gradients on isentropic surface.
Use equation 1.22 in [Holton, 1992] for horizontal gradient along isentropic surface:
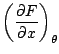 |
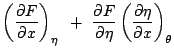 |
(4.4) | |
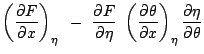 |
(4.5) |
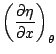 |
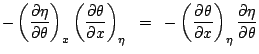 |
(4.6) |
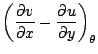 |
(4.7) | ||
![$\displaystyle \left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}...
...l \theta}{\partial y}\right)_{\eta}
\right] \frac{\partial\eta}{\partial\theta}$](img157.gif) |
(4.8) |
![$\displaystyle \frac{\partial}{\partial x}\left[T\left(\frac{p_0}{p}\right)^{\kappa}\right]$](img159.gif) |
(4.9) | ||
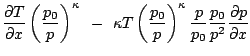 |
(4.10) | ||
![$\displaystyle \left(\frac{p_0}{p}\right)^{\kappa}
\left[ \frac{\partial T}{\partial x} - \kappa T \frac{\partial\ln p}{\partial x} \right]$](img161.gif) |
(4.11) |
![$\displaystyle \frac{\partial}{\partial p}\left[T\left(\frac{p_0}{p}\right)^{\kappa}\right]$](img163.gif) |
(4.12) | ||
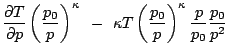 |
(4.13) | ||
![$\displaystyle \left(\frac{p_0}{p}\right)^{\kappa}
\left[ \frac{\partial T}{\partial p} - \kappa \frac{T}{p} \right]$](img165.gif) |
(4.14) |
| (4.21) |
| (4.22) |
In old preprocessing, an analog of (4.20) was implemented
with computed vorticity:
![]()
(4.23)
060, PV, Potential vorticity, K m2/kg/s
In ECMWF archive since 2000-07-18 ?
Seems to be only on presure levels and potential temperature levels.
3D field computed from temperature and pressure.
Definition according to [Holton, 1992, page 52]:
| (4.24) |
Equivalent latitude of pv on some selected theta levels:
300.0, 315.0, 330.0, 350.0, 370.0, 395.0, 475.0, 600.0, 850.0 K